Scarica tutti i 101 studi in formato PDF e sostieni il progetto Matepratica con soli 3,99€: clicca qui per effettuare il pagamento, riceverai subito un link via mail dove poter scaricare uno Zip con tutti gli studi pubblicati sul sito in versione PDF. Per ulteriori info scrivi a info@matepratica.it
Scarica tutti i 101 studi in formato PDF e sostieni il progetto Matepratica con soli 3,99€: clicca qui per effettuare il pagamento, riceverai subito un link via mail dove poter scaricare uno Zip con tutti gli studi pubblicati sul sito in versione PDF. Per ulteriori info scrivi a info@matepratica.it


Come si calcola limite e derivata di
e ^4x^2+3x-5
Perchè nella derivata prima cambi il segno e non p +2e^-x?
Questo commento è stato eliminato dall’autore.
Ciao volevo chiederti perchè nella derivata prima studi solo il numeratore e tralsci il denominatore, se non lo fai e poni Denominatore : e^(x)>0 poi si invertono i segni quando lo unisci con il numeratore…
ciao perchè e^x+2e^-x diventa poi nell asintoto obliquo e derivata e^x-2e^-x
grazie!gentilissimo.
Ciao Albert,scusa l’intromissione,ma come mai la derivata prima non è e^x+2e^-x,visto che la derivata dell’esponenziale è la funzione stessa?
e^(-x) è una funzione composta: devi anche moltiplicare per la derivata della funzione interna (esponente -x) quindi ottieni e^(-x)*(-1)=-e^(-x).
In totale f'(x)=e^x-2e^(-x)
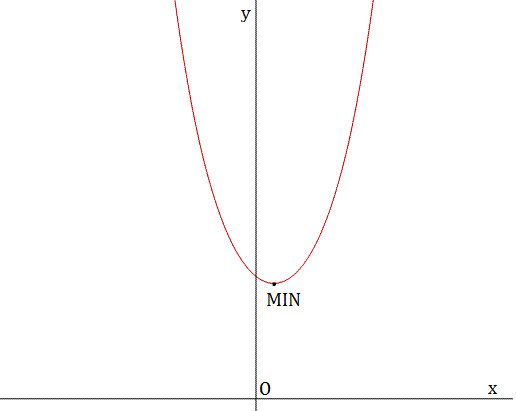
Certo che la funzione passa nel punto (0;3): nell’intersezione con gli assi affermo che (0;3) appartiene ad f(x), e anche dal grafico si nota…
Ciao Albert, mi chiedevo perchè la funzione non passa nel punto (0,3)
grazie..
Lo faccio, ma concludo subito che è sempre positiva perchè somma di funzioni esponenziali…
Ciao. Nello studio della derivata prima imponi f'(x)>0 e quindi
fai dei calcoli per trovarti il minimo giusto? Quello che non
capisco è perchè non fai la stessa cosa nella derivata seconda?
Grazie mille!!
Ciao Anonimo,
il minimo viene per x=ln(rad2), mentre per una dimenticanza avevo scritto ln2 (ora ho corretto). In ogni caso per trovare la y del minimo si sostituisce x=ln(rad2) nella funzione iniziale:
y = e^(ln(rad2)) +2e^(-ln(rad2))
y = rad2 +2/e^(ln(rad2))
y = rad2 +2/rad2
y = rad2 +(2rad2)/2
y = rad2 +rad2
y = 2rad2
quando hai calcolato f(ln2), come sei arrivato a 2rad(2)? Grazie
Ce ne sono un po’…quali in particolare?
Ciao, scusa la domanda stupida, ma non mi sono chiari i passaggi che hai fatto nel calcolo del minimo
Ciao,
(ln2)/2=
=(1/2)ln2= con proprietà dei logaritmi
=ln(2^(1/2))= visto che 2^(1/2)=rad2
=ln(rad2)
sono abbastanza negata in matematica quindi magari la mia domanda ti sembrerà stupida…ma perché ln2/2 è uguale a ln di radice di 2?