Scarica tutti i 101 studi in formato PDF e sostieni il progetto Matepratica con soli 3,99€: clicca qui per effettuare il pagamento, riceverai subito un link via mail dove poter scaricare uno Zip con tutti gli studi pubblicati sul sito in versione PDF. Per ulteriori info scrivi a info@matepratica.it
Studiamo la funzione
\[
f(x)=x^{\frac{3}{5-4x}}
\]
Dominio, asintoti e simmetrie
\[
5-4x\neq 0\rightarrow x \neq\frac{5}{4}
\]
\[
\mathcal{D}: \left(-\infty; \frac{5}{4}\right)\bigcup\left(\frac{5}{4};+\infty\right)
\]
Non sono presenti simmetrie evidenti.
Comportamento agli estremi del dominio
\[
\lim_{x\to \frac{5}{4}^-}xe^{\frac{3}{5-4x}}=\frac{5}{4}e^{\frac{3}{0^+}}=\frac{5}{4}e^{+\infty}=+\infty
\]
\[
\lim_{x\to \frac{5}{4}^+}xe^{\frac{3}{5-4x}}=\frac{5}{4}e^{\frac{3}{0^-}}=\frac{5}{4}e^{-\infty}=0
\]
\(x=\frac{5}{4}\) Asintoto verticale (sinistro)
\[
\lim_{x \to -\infty}xe^\frac{3}{5-4x}=-\infty e^0=-\infty
\]
Non esiste l’asintoto orizzontale, potrebbe esistere l’asintoto obliquo \(y=mx+q\).
Ricerco \(m\):
\[
m=\lim_{x\to \pm \infty} \frac{f(x)}{x}=\lim_{x\to -\infty}\frac{xe^{\frac{3}{5-4x}}}{x}=\lim_{x \to -\infty}e^{\frac{3}{5-4x}}=e^0=1
\]
Ricerco \(q\):
\[
q=\lim_{x \to\pm \infty}f(x)-mx=\lim_{x \to-\infty}xe^{\frac{3}{5-4x}}-x=\lim_{x\to -\infty}x \left(e^{\frac{3}{5-4x}}-1\right)=-\infty\cdot 0 \hspace{5 mm}\text{Forma indeterminata}
\]
Bisogna operare in modo tale da poter ricondurre il limite in una forma nota.
Si procede per sostituzione, quindi si pone
\[
t=\frac{3}{5-4x} \hspace{5mm}\text{se}\hspace{3mm}x\rightarrow – \infty \hspace{5mm}t \rightarrow0^+
\]
Si ricava \(x\)
\[
\frac{5-4x}{3}=\frac{1}{t} \hspace{3mm}\rightarrow\hspace{3mm} 5-4x=\frac{3}{t}\hspace{3mm} \rightarrow\hspace{3mm} 4x=\frac{5t-3}{t}\hspace{3mm}\rightarrow\hspace{3mm} 4tx=5t-3 \hspace{3mm}\rightarrow\hspace{3mm} x=\frac{5t-3}{4t}
\]
Si può ora scrivere il limite in questo modo
\[
q=\lim_{t\to 0^+}\frac{5t-3}{4t}\left(e^t -1\right)=\lim_{t\to 0^+}\frac{5t-3}{4}\cdot \lim_{t \to 0^+}\frac{e^t -1}{t}=-\frac{3}{4}
\]
dove \(\lim_{t \to 0^+}\frac{e^t -1}{t} \) è un limite notevole e vale 1.
Del tutto analogo è il procedimento per \(x \rightarrow +\infty \). Quindi \(y=x-\frac{3}{4}\) è asintoto obliquo.
Segno della funzione
\[
f(x)>0 \hspace{5mm}\rightarrow\hspace{5mm} xe^{\frac{3}{5-4x}}>0 \text{per} \hspace{5mm} x>0
\]
Significa che la funzione è positiva e negativa negli intervalli \(I_p\) e \(I_n\) rispettivamente.
\[
I_p \left(0;\frac{5}{4}\right)\bigcup\left(\frac{5}{4};+\infty\right), \hspace{3mm} I_n \left(-\infty;0\right)
\]
Intersezione con gli assi
\[
f(0)=0
\]
\[
f(x)=0 \hspace{3mm}\text{per}\hspace{3mm}x=0.
\]
La funzione, quindi, interseca gli assi all’origine \(O(0,0)\)
Punti di massimo, minimo e flesso
\begin{align*}
f'(x)&=e^{\frac{3}{5-4x}}+e^{\frac{3}{5-4x}}\cdot\frac{12}{(5-4x)^2}=\\
&=e^{\frac{3}{5-4x}}+\frac{12xe^{\frac{3}{5-4x}}}{(5-4x)^2}=\\
&=\frac{(5-4x)^2 e^{\frac{3}{5-4x}}+12xe^{\frac{3}{5-4x}}}{(5-4x)^2}=\\
&=e^{\frac{3}{5-4x}}\left[(5-4x)^2 +12x\right]=\\
&=\frac{e^{\frac{3}{5-4x}}(16x^2 -28x+25)}{(5-4x)^2}
\end{align*}
\[
f'(x)=0 \hspace{5mm} e^{\frac{3}{5-4x}}(16x^2 -28x+25)=0 \hspace{3mm}\text{mai verificata}
\]
La derivata prima non si annulla mai, dunque la funzione non possiede punti di massimo o di minimo.
\begin{align*}
&f'(x)>0 \hspace{5mm} e^{\frac{3}{5-4x}}\hspace{2mm}\forall x\in D
&(16x^2 -28x+25)>0 \hspace{2mm}\forall x \in D
&(5-4x)^2>0 \hspace{2mm }\forall x\in D
\end{align*}

Bisogna ora determinare eventuali punti di flesso e le concavità.
Svolgendo i calcoli si ottiene
\[
f”(x)=\frac{24e^{\frac{3}{5-4x}}(25-14x)}{(4x-5)^4}\hspace{3mm}\rightarrow\hspace{3mm}f”(x)=0 \hspace{1mm} \text{per}\hspace{1mm} x=\frac{25}{14}
\]
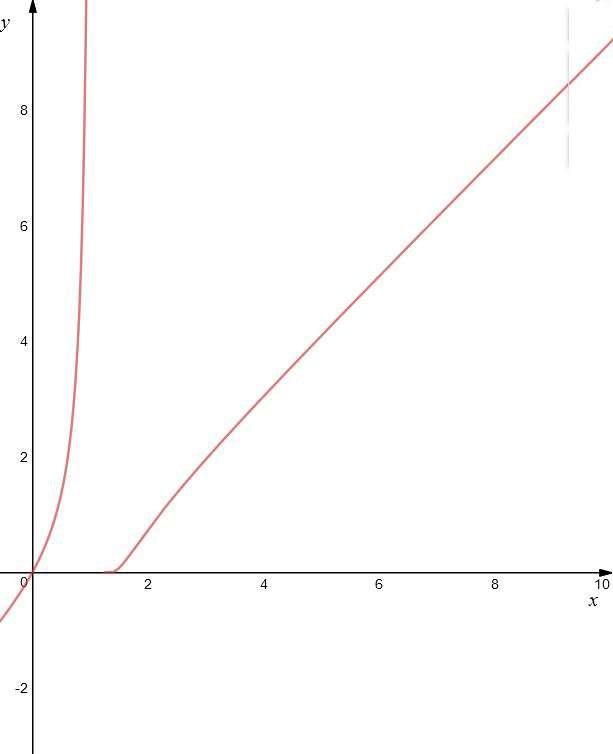
Si ha quindi un punto di flesso a tangente obliqua in \(F\left(\frac{25}{14};f(\frac{25}{14})\approx (1.78;0.44)\right)\).

\(f”(x)>0 \hspace{1 mm}\text{per}\hspace{1mm}x<\frac{25}{14}\)
Scarica tutti i 101 studi in formato PDF e sostieni il progetto Matepratica con soli 3,99€: clicca qui per effettuare il pagamento, riceverai subito un link via mail dove poter scaricare uno Zip con tutti gli studi pubblicati sul sito in versione PDF. Per ulteriori info scrivi a info@matepratica.it
C’è un errore nel dominio: la base di una funzione f(x)^g(x), deve essere posta >0 (ossia f(x) > 0), cosa che qui manca, se potete correggete
Guardando il resto, ossia oltre il dominio, ho visto che l’errore, meno grave, è nella scrittura iniziale della f(x): rispetto a quella che sviluppate manca una e (numero di Nepero)