Scarica tutti i 101 studi in formato PDF e sostieni il progetto Matepratica con soli 3,99€: clicca qui per effettuare il pagamento, riceverai subito un link via mail dove poter scaricare uno Zip con tutti gli studi pubblicati sul sito in versione PDF. Per ulteriori info scrivi a info@matepratica.it
Studiare la seguente funzione: \[ f\left(x\right)=\frac{1+x}{1-\left|x\right|} \] Innanzitutto la funzione si può anche scrivere in questo modo:
Se \[ x\geq0 \] allora: \[ f\left(x\right)=\frac{1+x}{1-x} \] Se \[ x<0 \] allora: \[ f\left(x\right)=\frac{1+x}{1+x}\rightarrow f\left(x\right)=1 \] 1) Dominio: \[ 1-\left|x\right|\neq0\rightarrow\left|x\right|\neq1\rightarrow x\neq\pm1 \] \[ D=R-\left\{ \pm1\right\} \] 2) Simmetrie: \[ f\left(-x\right)=\frac{1-x}{1-\left|-x\right|}=\frac{1-x}{1-\left|x\right|} \] \[ f\left(-x\right)\neq f\left(x\right) \] \[ f\left(-x\right)\neq-f\left(x\right) \] f(x) non è ne pari ne dispari.
3) Intersezioni con gli assi: \[ \left\{ \begin{array}{c} x=0\\ f\left(x\right)=1 \end{array}\right.\rightarrow\left(0;1\right)\in f\left(x\right) \] 4) Segno:
Avremo due casi:
a) x>0 \[ f\left(x\right)\geq0 \] \[ \frac{1+x}{1-x}\geq0 \] \[ \left\{ \begin{array}{c} Num\geq0\rightarrow x\geq-1\\ Den>0\rightarrow x\leq+1 \end{array}\right. \] Ora, ricordandoci che stiamo studiando la funzione per x>0, scopriamo che il numeratore è sempre positivo, mentre il denominatore è positivo tra 0 e 1, e negativo per x>1. Di conseguenza per x>0 la funzione prenderà il segno del denominatore: \[ Intervallo\;\left(0;1\right)\rightarrow f\left(x\right)>0 \] \[ Intervallo\;\left(1;+\infty\right)\rightarrow f\left(x\right)<0 \] b) x<0:
In questo caso f(x)=1, è una retta orizzontale ad altezza 1, quindi è sempre positiva.
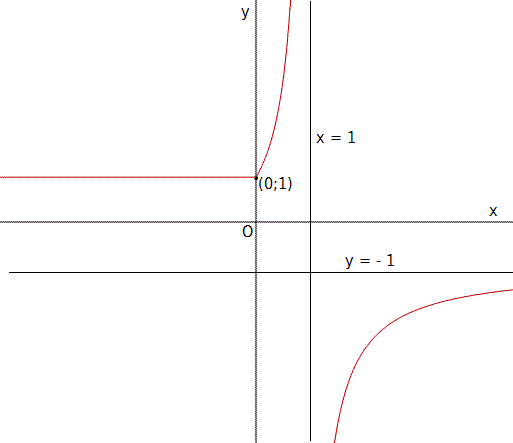
5) Limiti: \[ \lim_{x\rightarrow+\infty}f\left(x\right)=-1 \] y=-1 è un asintoto orizzontale. \[ \lim_{x\rightarrow1^{\pm}}f\left(x\right)=\left[\frac{2}{0^{\mp}}\right]=\mp\infty \] x=1 è un asintoto verticale. \[ \lim_{x\rightarrow-1^{\pm}}f\left(x\right)=1 \] Per x=-1 si ha quindi un punto di discontinuità di terza specie (o eliminabile, c’è un “buco” nella funzione). NB: nel grafico rappresentato sotto, questo punto (1;1) NON è evidenziato, ma c’è :)
6) Derivate:
Avremo due casi:
a) Intervallo x>0: \[ f’\left(x\right)=\frac{1-x-\left(1+x\right)\left(-1\right)}{\left(1-x\right)^{2}}=\frac{1-x+1+x}{\left(1-x\right)^{2}}=\frac{2}{\left(1-x\right)^{2}} \] \[ f’\left(x\right)\geq0\;\forall x\in D-\left\{ 1\right\} \] quindi f'(x), quando esiste, è sempre positiva per x>0, di conseguenza in questo intervallo f(x) è crescente.
b) Intervallo x<0:
In questo intervallo la funzione vale 1 quindi (f'(x)=0) ed è costante.
Possiamo notare che: \[ f’\left(0\right)=2 \] \[ \lim_{x\rightarrow0^{-}}f’\left(x\right)=0 \] \[ \lim_{x\rightarrow0^{-}}f’\left(x\right)\neq f’\left(0\right) \] quindi in (0;1) abbiamo un punto angoloso.
Derivata seconda, i due casi:
a) Intervallo x>0: \[ f”\left(x\right)=\frac{-2\cdot2\left(1-x\right)\left(-1\right)}{\left(1-x\right)^{4}}=\frac{4\left(1-x\right)}{\left(1-x\right)^{4}} \] facendo i conti: \[ f”\left(x\right)\geq0\rightarrow1-x\geq0\rightarrow x<1 \] quindi, per x>0, la funzione risulta convessa nell’intervallo (0;1), concava nell’intervallo x>1.
b) x<0: \[ f”\left(x\right)=0 \] Come sappiamo la funzione per x<0 vale 1, è costante, quindi ne concava ne convessa.
Scarica tutti i 101 studi in formato PDF e sostieni il progetto Matepratica con soli 3,99€: clicca qui per effettuare il pagamento, riceverai subito un link via mail dove poter scaricare uno Zip con tutti gli studi pubblicati sul sito in versione PDF. Per ulteriori info scrivi a info@matepratica.it
ma nello studio del segno perche’ hai posto il denominatore >= a 0? Viene 1 e 1 e’ escluso dato che annulla la funzione al denominatore.
grazie in anticipo
ciao, perché non viene fatto il limite che tende a meno infinito?
Salve. Vorrei sapere perché nell’intersezione con gli assi non ha considerato anche per Y=0 oltre che per x=0. Grazie in anticipo.
Salve. Vorrei sapere perché nell’intersezione con gli assi non ha considerato anche per Y=0 oltre che per x=0. Grazie in anticipo.
Salve. Vorrei sapere perché nell’intersezione con gli assi non ha considerato anche per Y=0 oltre che per x=0. Grazie in anticipo.
Alla frase “ora ricordandoci.. ..” penso tu abbia scambiato di posto le parol numeratore e denominatore… Infatti il Denominatore è sempre positivo (considerando x>0 come valore assoluto), invece il numeratore è positivo tra 0 e 1, e negativo per x>1
No è giusto così: per x>0 il valore assoluto non c’è e rimane 1-x
Ma quando studio la funzione esponenziale elevata ad un valore assoluto devo sempre distinguere i due casi per tto lo studio??? Grazie
Se la funzione è e^|x| allora è pari e la puoi studiare tutta per x>0, ovvero e^x… poi la parte a sinistra dell’asse y sarà simmetrica rispetto all’asse y.
Se la funzione è e^|f(x)| in generale si, devi fare i due casi.
ciao, perchè il limite della funzione a -1 è 1 ?
Perchè per x=-1 la funzione non esiste, ma so che per tutte le x<0 la funzione vale 1 (quindi anche per tutte le x in un intorno piccolo a piacere di -1).
La funzione da studiare per x<0 è uguale a una costante, in particolare vale:
f(x) = 1
(è una retta parallela all’asse x)
La derivata di un numero è zero:
f'(x) = 0
(infatti una retta orizzontale ha coefficiente angolare m=0)
per piacere, mi puoi spiegare la derivata prima per x<0? Sono in difficoltà…