Inscrivere in un dato semicerchio il quadrilatero di superficie massima con un lato parallelo al diametro.

Soluzione

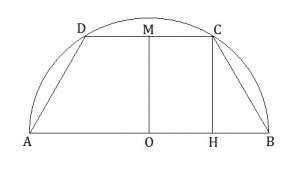
Rappresentiamo un semicerchio, e notiamo che il quadrilatero inscritto richiesto risulta un trapezio isoscele:

Vista la figura, chiamiamo: \[ \overline{OC}=\overline{OB}=r\rightarrow\overline{AB}=2r \] \[ \overline{OM}=\overline{CH}=h \] \[ \overline{DC}=b\rightarrow\overline{MC}=\overline{OH}=\frac{b}{2} \] La superficie del trapezio è \[ A=\frac{\left(\overline{AB}+\overline{DC}\right)\cdot\overline{CH}}{2} \] \[ A=\frac{h\left(2r+b\right)}{2} \] Considerando il triangolo rettangolo OCH possiamo trovare h in funzione di b, grazie al teorema di Pitagora: \[ h=\sqrt{r^{2}-\left(\frac{b}{2}\right)^{2}}\rightarrow h=\sqrt{r^{2}-\frac{b^{2}}{4}} \] Ora possiamo scrivere l’area in funzione di una sola variabile (b): \[ A\left(b\right)=\frac{1}{2}\sqrt{r^{2}-\frac{b^{2}}{4}}\cdot\left(2r+b\right) \] \[ A\left(b\right)=\frac{1}{4}\sqrt{4r^{2}-b^{2}}\cdot\left(2r+b\right) \] Calcoliamo la derivata: \[ \frac{dA}{db}=\frac{1}{4}\left[\frac{-2b\left(2r+b\right)}{2\sqrt{4r^{2}-b^{2}}}+\sqrt{4r^{2}-b^{2}}\right] \] \[ \frac{dA}{db}=\frac{-2rb-b^{2}+4r^{2}-b^{2}}{4\sqrt{4r^{2}-b^{2}}} \] \[ \frac{dA}{db}=\frac{-2b^{2}-2rb+4r^{2}}{4\sqrt{4r^{2}-b^{2}}} \] Studiamone il segno: \[ \frac{dA}{db}\geq0\rightarrow-2b^{2}-2rb+4r^{2}\geq0 \] perchè il denominatore è positivo. \[ \frac{dA}{db}\geq0\rightarrow b^{2}+rb-2r^{2}\leq0 \] Facendo i conti, e ricordandoci che b non può essere negativo, otteniamo: \[ \frac{dA}{db}\geq0\rightarrow b\leq r \] Abbiamo trovato l’intervallo di b per il quale la derivata della funzione A è positiva. La funzione A(b) è crescente per b minore di r, decrescente per b maggiore di r, ha quindi un massimo per \[ b=r \] Quindi risulta \[ \overline{DC}=r \] \[ \overline{MC}=\overline{OH}=\overline{HB}=\frac{r}{2} \] I triangoli OHC e CHB sono quindi congruenti, in particolare \[ \overline{CB}=\overline{AD}=r=\overline{DC} \] e il trapezio è un semiesagono regolare.