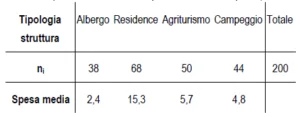
In una località turistica si osserva la seguente distribuzione di 200 turisti secondo le tipologie di strutture ricettive, per ciascuna delle quali è fornito anche l’importo mediamente speso (in centinaia di euro) da ogni turista:

a) Determinare il grado di eterogeneità presente nella distribuzione di frequenza, nonché la moda.
b) Determinare la spesa mediamente sostenuta da tutti i 200 turisti.
c) Sapendo che la varianza degli importi spesi dai 200 turisti vale 1978,5656 determinare la varianza interna (o residua) di tali importi.
d) Considerando i 200 turisti come un campione casualmente estratto da una popolazione più vasta, stimare l’intervallo di confidenza al livello 1-\[\alpha\]=0,98 per la spesa media di popolazione.

Soluzione

a) Per calcolare il grado di eterogeneità della distribuzione di frequenza bisogna calcolare l’indice di Gini assoluto:
\(G=1-\sum_{i=1}^4f_{r_i}^2\)
dove \(f_{r_i}^2\) sono le frequenze relative:
\[\begin{eqnarray}
f_{r_1}&=&\frac{38}{200}=0.19\\
f_{r_2}&=&\frac{68}{200}=0.34\\
f_{r_3}&=&\frac{50}{200}=0.25\\
f_{r_4}&=&\frac{44}{200}=0.22\end{eqnarray}\]
Dunque otteniamo:
\(G=1-(0.19^2+0.34^2+0.25^2+0.22^2)=0.7374\)
Per avere un’informazione più precisa riguardo al grado di eterogeneità, si calcola l’indice di Gini relativo. Indicando con \(k=4\) il numero di categorie presenti nella distribuzione, risulta:
\(G_N=\frac{G}{\frac{k-1}{k}}=\frac{0.7374}{\frac{3}{4}}=0.9832\)

Essendo tale indice compreso tra 0 e 1, possiamo dire che l’eterogeneità della distribuzione è molto alta, ossia, che le scelte relative al tipo di struttura turistica sono molto simili tra di loro.

La l’moda è banalmente il “Residence” dato che è il tipo di alloggio maggiormente preferito dai turisti (68).

b)La spesa media sostenuta da tutti i turisti è:
\(\mu=\frac{2.4*38+15.3*68+5.7*50+4.8*44}{200}=8.139\)

c) Calcoliamo dapprima la varianza tra i gruppi:
\(VAR_{tra}=\frac{38(2.4-8.139)^2+68(15.3-8.139)^2+50(5.7-8.139)^2+44(4.8-8.139)^2}{4-1}=1842.1986\)

Adesso, sapendo che \(VAR_{tot}=1978.5656\), possiamo usare la formula di scomposizione della varianza

\(VAR_{entro}=VAR_{tot}-VAR_{tra}=1978,5656-1842.1986=136.367\)

d) Dato che il campione è molto grande, possiamo sostituire la varianza della popolazione incognita con la varianza campionaria \(\sigma^2=1978.5656\).
Inoltre, il valore critico corrispondente al valore $\alpha = 0.02$ è: \(z_{1-\frac{\alpha}{2}}=z_{0.99}=2.33\).
Dunque, l’intervallo di confidenza per la spesa media è dato da:
\[\begin{eqnarray}
\overline{x} &\pm & z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\\
8.139&\pm & 2.33\frac{\sqrt{1978.5656}}{\sqrt{200}}\\
8.139&\pm & 7.33\end{eqnarray}\]
da cui si ottiene \(I=(0.809,15.469)\)