Testo

Nel piano riferito a coordinate cartesiane, ortogonali e monometriche, si tracci il grafico Gf della funzione f(x) logaritmo naturale.

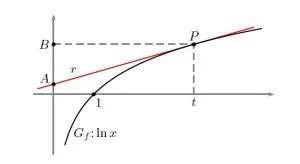
1. Sia A il punto d’intersezione con l’asse y della tangente a G in un suo punto P. Sia B il punto d’intersezione con l’asse y della parallela per P all’asse x. Si dimostri che, qualsiasi sia P, il segmento AB ha lunghezza costante. Vale la stessa proprietà per il grafico Gg della funzione g(x) logaritmo in base a (con a reale positivo diverso da 1) di x?

2. Si consideri l’inclinazione sull’asse x della retta tangente a Gg nel suo punto di ascissa 1. Per quale valore della base a questa inclinazione risulta essere di 45 gradi? E per quale valore invece è di 135 gradi?

3. Sia D la regione del primo quadrante delimitata dagli assi coordinati, da Gf e dalla retta d’equazione y = 1. Si calcoli l’area di D.

4. Si calcoli il volume del solido generato da D nella rotazione completa attorno alla retta d’equazione x = 1.

Soluzione

1. La funzione logaritmo naturale con dominio R+ \[ f\left(x\right)=\ln x \] ha il seguente grafico:

Se P(t, lnt) è un punto qualsiasi di questa funzione, l’equazione della retta tangente in P è: \[ y-\ln t=\frac{1}{t}\left(x-t\right) \] L’ordinata di A, punto di intersezione con l’asse y di r, si ottiene ponendo x = 0 in: \[ y_{A}-\ln t=\frac{1}{t}\left(0-t\right)\rightarrow y_{A}=-1+\ln t \] L’ordinata di B è: \[ y_{B}=y_{P}=\ln t \] E la lunghezza di AB è: \[ AB=|y_{B}-y_{A}|=|\log_{a}t-\left(\log_{a}t-\frac{1}{\ln a}\right)=|\frac{1}{\ln a}|=|\log_{a}e| \] La lunghezza del segmento risulta essere indipendente dalla posizione di P.

2. L’interpretazione geometrica della derivata prima della funzione g è la tangente goniometrica dell’angolo che la retta tangente forma con il semiasse positivo delle x.

Poichè per il punto di ascissa 1 abbiamo un angolo di 45, poniamo: \[ g’\left(1\right)=\tan\delta\rightarrow\tan45=\frac{1}{1*\ln a}=1\rightarrow\ln a=1\rightarrow a=e \] Invece per un angolo di 135 gradi avremo che: \[ g’\left(1\right)=\tan\delta\rightarrow\tan135=\frac{1}{1*\ln a}=-1\rightarrow\ln a=-1\rightarrow a=\frac{1}{e} \]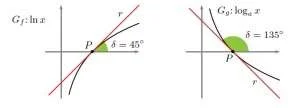

3. Definito il punto A come il punto di Gf avente ordinata pari a 1, l’area della regione finita D si ottiene per differenza tra l’area del rettangolo avente i lati paralleli agli assi coordinati vertici opposti O ed A e l’area del trapezoide E definito da Gf con x compreso tra 1 e l’ascissa del punto A. Pertanto sapendo che l’ordinata del punto A è pari a 1, si ottiene: \[ \ln x=1\rightarrow x_{A}=e\rightarrow A\left(D\right)=x_{A}*y_{A}-\int_{1}^{e}\ln xdx=x_{A}*y_{A}-\left[x\ln x-x\right]_{1}^{e} \] \[ A\left(D\right)=\left(e-e\right)-\left(0-1\right)=1\rightarrow A\left(D\right)=e-1 \]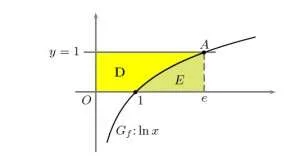

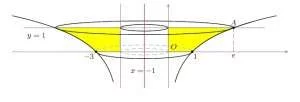
4. Poichè viene chiesto il volume di un solido di rotazione attorno alla retta verticale x = 1 conviene scambiare i ruoli di x e y con la trasformazione seguente: \[ \left\{ \begin{array}{c} x’=y\\ y’=x \end{array}\right. \] Risulta quindi che x’ = ln y’ ossia, esplicitando y’: \[ y’=e^{x’} \] Con tale trasformazione la retta di equazione x = -1 diviene y’ = -1 e l’immagine della regione D diventa la figura qui sotto

Infine, allo scopo di riportare questa retta a coincidere con l’asse x applichiamo la traslazione seguente: \[ \left\{ \begin{array}{c} y”=y’+1\\ x”=x’ \end{array}\right. \] per cui l’equazione della retta si riduce a y’ = 0 mentre la funzione diventa y” = 1 ossia \[ y”=1+e^{x”} \] Considerando la formula che fornisce il volume dei solidi di rotazione attorno all’asse delle x limitati dalla funzione ottengo l’integrale da cui ricavarmi il volume richiesto: \[ V=\int_{b}^{a}\left[f\left(x\right)\right]^{2}dx=\pi\int_{0}^{1}\left(1+e^{x}\right)^{2}dx-\pi=\pi\left[x+2e^{x}\right]_{0}^{1}+\pi\int_{0}^{1}e^{2x}dx-\pi \] Risolti gli integrali immediati rimane l’integrazione dell’ultimo termine. Inserendo un fattore costante pari a 2 questo si riscrive come: \[ \int e^{2x}dx=\frac{1}{2}\int e^{2x}\left(2dx\right)=\frac{1}{2}\int e^{2x}d\left(2x\right)=\frac{1}{2}e^{2x}+C \] \[ V=\pi\left(1+2e-2\right)+\frac{\pi}{2}\left[e^{2x}\right]_{0}^{1}-\pi=\frac{\pi}{2}\left(e^{2}+4e-5\right) \]